Two indicators primarily drive a bowler's success: the number of wickets taken and the average runs conceded per wicket.
In applying those yardsticks to judge bowlers by, we are homogenizing the wickets taken by all bowlers, as if to suggest that all wickets taken by any bowler are 'equivalent' in every sense. Most people would agree that the assumption is erroneous - a tail end wicket, to cite the obvious example, does not equate with that of a top class opener.
Surely, therefore, there are variable values that may be assigned to each wicket. For example, can the wicket of say Sachin Tendukar be ever equated with the one of say Ashish Nehra?
Yet, such a differentiation is necessary if we are to truly judge bowlers, to separate the men who slice through the cream of opposition batting from the boys who pick off the tail.
How then does one assess this dimension of bowling: the 'value of dismissals'? Are there some bowlers who have primarily got better batsmen out and others who have relished taking wickets of tail-enders?
The following paragraphs describe the methodology and the results of my attempt to gauge the value of a bowler's dismissals.
It is clear that dismissals made by a bowler have to be weighted by some factor that would represent the quality of the batsman. One possibility is to weight it by the number at which the batsman batted. So, for example, if Hayden bats at 1 and McGrath at 11, then their wickets taken by various bowlers could be weighted by 1 & 11 (or some arithmetic manipulation thereof) to differentiate between their capabilities.
The chief problem in that approach is that one essentially divides the entire batting population into eleven distinct groups. In the process, a Hayden becomes equivalent in weight to a Deep Dasgupta because both bat at # 1. Similarly, there could be good batsmen who come lower down in the order due to various reasons. Steve Waugh bats at # 5 or # 6, yet few would question that Waugh is better than most batsmen who bat higher in the order.
In order to make the analysis as comprehensive and objective as possible, the approach taken uses the career batting average of each batsman as the parameter to weight the value of his wicket.
With this approach, the objective is to find the "weighted batting average per dismissal" for each bowler. If this number is much lower for one bowler than for another bowler, then the former has got more of his wickets from lower-order batsmen with lower batting averages than the latter. The methodology employed was thus as follows:
1) The career batting records of every player in cricket history were taken
2) The top 20 wicket-taking bowlers of all-time were selected for analysis: Trueman was taken out of consideration since he played in a different era, and Bedi was included more out of curiosity.
3) For each bowler, the actual dismissal by batsmen was analyzed.
4) The career average of each batsman dismissed by a particular bowler was weighted by the number of times he was dismissed by that bowler. This weighted product was divided by the number of dismissals to get a "weighted batting average per dismissal".
To elucidate this, consider an example: A bowler, say A, has taken 10 wickets in his career; including 7 times the wicket of Batsmen X who has had a career batting average of 50 and 3 times of Batsmen Y who has had a career batting average of 10.
The "weighted batting average per dismissal" is calculated as (50 X 7 + 10 X 3)/10 = 38. This means that on an average, Bowler A has dismissed batsmen with a batting average of 38. Across a very high number of dismissals, this reasonably reflects on an average the quality of the batsmen dismissed.
The results are tabulated below. Let's take an example to be fully clear of what these numbers mean:
On an average, Richard Hadlee dismissed batsmen with a batting average of 29.55 runs per innings, while Muralitharan dismissed batsmen with a batting average of 27.42, nearly two runs lower than Hadlee.
So comparatively, Hadlee got `better' batsmen out than did Murali. These numbers do seem to be very close to each other, but that is largely due to the fact that they are weighted averages of a large set of numbers.
To appreciate what these differences mean, we need to look at the `distribution' rather than just the averages. For example, Dennis Lillee took only 8 wickets of batsmen with an average of <10, while Akram did so on 66 occasions. Yet, the difference between their "weighted batting average per dismissal" is a mere 5 runs.
So, from the distribution, it is clear that Lillee got much fewer wickets of tail-enders, while Akram relished those opportunities. Continuing this comparison, 60% of Lillee's dismissals came of batsmen whose batting averages were > 30, while only 40% of Akram's dismissals came from that group. This is another piece of evidence that Lillee specialized in getting the top and middle order, while Akram enjoyed polishing off the tail.
Bowlers who got `better' batsmen out are Lillee, McDermott, Ambrose, Marshall, Gibbs and Underwood. There are many more on the mid-range like Kapil, Hadlee, Imran etc. The bowlers who dismissed batsmen with a lower batting average were Akram, Waqar and Murali.
The bowlers who made it to the first list could have done so due to a variety of reasons, the chief ones being either intrinsically good quality bowling or the absence of other good bowlers. For example, Lillee, Ambrose and Marshall are good examples of bowlers who got these `better' batsmen out in spite of there being other good bowlers in the side. However, it could perhaps be argued that bowlers like McDermott and even Kapil benefited from the fact that there weren't too many other good bowlers in the side, and hence they had a better opportunity to get any batsman out.
It needs to be clarified here that having a higher "weighted batting average per dismissal" does not in any way make one bowler superior or more of a match-winner than another. Maybe polishing off the tail was far more important in many cases than getting top and middle order batsmen were in other situations.
| Name | Weighted Batting Avg per Dismissal |
| CA Walsh | 29.66 |
| SK Warne | 28.29 |
| M Muralitharan | 27.42 |
| N Kapil Dev | 29.81 |
| RJ Hadlee | 29.55 |
| GD McGrath | 29.79 |
| Wasim Akram | 26.34 |
| CEL Ambrose | 30.15 |
| IT Botham | 29.32 |
| MD Marshall | 30.49 |
| Waqar Younis | 27.78 |
| Imran Khan | 29.90 |
| A Kumble | 28.33 |
| DK Lillee | 31.27 |
| AA Donald | 29.59 |
| RGD Willis | 29.96 |
| SM Pollock | 28.92 |
| LR Gibbs | 30.45 |
| DL Underwood | 31.50 |
| CJ McDermott | 31.37 |
| BS Bedi | 28.95 |
But many may argue, and rightly so, that some bowlers may never have got as much opportunity to bowl to batsmen with a high batting average as others did. Two typical reasons could be: countries against whom matches were played, and the presence of other good quality bowlers in the side.
For example, Shane Warne could complain of not getting as much of a chance to bowl to good batsmen as say Glen McGrath. Surely, the average of batsmen that Glen McGrath has dismissed is about two runs higher than that of Shane Warne. So, why fault Warne?
That is a valid argument. To augment the analysis, one can then look at the average runs conceded per dismissal. For example, Ambrose's dismissals were on an average of batsmen with an average of 30.15 runs per innings, while he conceded only 20.99 runs for dismissing each of them. Hence Ambrose managed to "discount" the average of the batsmen he dismissed. Compare that with say Anil Kumble whose weighted batting average per dismissal was 28.33, but he conceded 28.21 runs per such dismissal. Clearly he hasn't discounted batsmen's averages as much as Ambrose has done.
Juxtaposing both these parameters on a single matrix, gives a good picture:
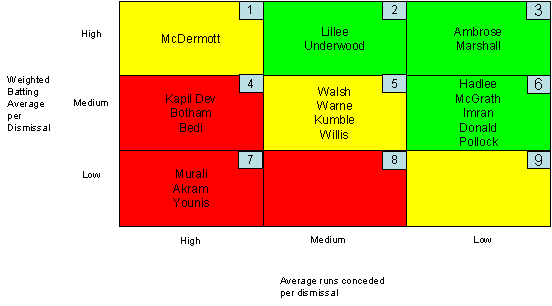
One can think of the two axes as: "Y" axis representing value of the wicket (quality of the batsman dismissed) and "X" axis representing the price of the wicket (runs conceded per dismissal).
So, the matrix can be treated as a classic value-price matrix. In such a matrix, areas 1, 5 and 9 are "normal" areas: where a bowler has conceded runs in a fair proportion with the quality of batsmen dismissed: Value is proportional to price.
Areas 2, 3 & 6 are "super-normal" areas, where bowlers have done better than normal by getting better quality batsmen out for less runs per dismissal. Greater value for lower price.
Areas 4, 7 & 8 are "sub-normal" where bowlers have given away more runs per dismissal than is warranted by the quality of batsmen they have dismissed. Lower value for a higher price.
Clearly, Ambrose and Marshall out-perform everyone else. Murali, Akram and Younis under-perform by getting lower order batsmen out but paying a disproportionately high price for it.
But this 3X3 matrix is prepared largely using artificial divisions of Low, Medium and High on both axes. These could in some cases lead to a misleading picture with a bowler or two moving into higher or lower categories very marginally.
To get a clearer picture, we can simply introduce another derived metric: the discount that a bowler achieves defined as the average runs conceded by the bowler per dismissal as a percentage of the weighted batting average per dismissal. The term "Dismissal Quotient" is abstruse enough, so let's use it:
Dismissal Quotient = (Average runs per dismissal) / (Weighted Batting Average per Dismissal) *100
For Ambrose, for example the Dismissal Quotient is = 20.99 / 30.15 = 70%. This means, in other words that Ambrose managed to discount the batsmen's score by 30% compared to what these batsmen have scored through their careers.
| Bowler | Dismissal Quotient |
| Marshall | 69% |
| Ambrose | 70% |
| Pollock | 72% |
| McGrath | 73% |
| Hadlee | 75% |
| Donald | 75% |
| Imran | 76% |
| Lillee | 76% |
| Walsh | 82% |
| Underwood | 82% |
| Willis | 84% |
| Waqar | 85% |
| Murali | 86% |
| Akram | 90% |
| Warne | 91% |
| McDermott | 91% |
| Gibbs | 96% |
| Botham | 97% |
| Kapil Dev | 99% |
| Kumble | 100% |
| Bedi | 100% |
There seem to be five clusters of bowlers, not very dissimilar to the ones obtained in the 3X3 described above.
It is worth reiterating that with this statistic, one can understand bowling performance better than without it. However, it is by no means a comprehensive statistic, nor is it necessarily indicative of the match-winning abilities of a particular bowler.
And finally, statistics are a vehicle for dispassionate observation. They don't naturally look beneath the numbers. For example, Bedi's dismissal quotient of 100% may look unfavorable compared to Ambrose or Marshall, but it is well understood that Bedi had to "buy" wickets due to the little support he had from fast bowlers from his team. Also Kapil's numbers have to be understood in the context of the fact that he bowled a lot in India, on indifferent pitches which gave him very little assistance.
Having said that, this analysis does bring to light the greatness of the two West Indian quicks and McGrath and Pollock, who not only are among the 20 highest wicket-takers ever, but also managed to rip through high-quality batting orders at a low price.
Marshall, one may argue, operated in a time when the West Indians were dominant in world cricket. So, he did enjoy the benefit of pressuring the high-order batsmen due to a high score put up by his team or the expectation thereof. The same is true for Glen McGrath too. But Ambrose shines in spite of bowling for a large part in an era when West Indian domination was waning. In some sense, his statistics are even more creditable.
In sum, one can say that in addition to other reasons, this statistic should support the claim of these four bowlers as being among the all-time greats in cricket.
Subodh S. Chitre can be reached at schitre@hotmail.com








